The binomial distribution model allows us to compute the probability of observing a specified number of "successes" when the process is repeated a specific number of times (e.g. in a set of students grade) and the outcome for a given student's grade is either a success or a failure.

There are few Pre-requisites for binomial distribution

1. There are two potential outcomes per trail.

2. The probability of success (p) is same across all the trails.

3. The number of trails (n) is fixed.

4. Each trail is independent.

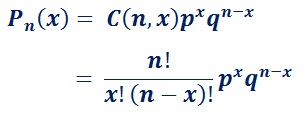Binomial Distribution Formula.

where
n = the number of trails.
x = the number of successes desired.
p = probability of getting a success in one trail.
q = 1-p = the probability of getting a failure in one trail.

To understand binomial distribution will consider an example of students grade in an examination. 40% of students pass in this examination. Will take random 10 students

I have taken this example as it satisfies all the Pre-requisites mentioned above.

There are two outcomes in this example i.e. student can either Pass or Fail.

The probability of success is same.

The number of students is fixed.

A student will pass or fail will depend on his or her marks.

We will find the probability in different scenarios.

1. All student passed the examination.

As there are 10 students so if all the students pass the probability would be

2. No student passed the examination.

As there are 10 students so if all the students didn't pass (1-0.4) the probability would be

3. Only two students passed the examination.

As two students passed out of ten therefore C(10,2) ways.

Now compare the above equation with the binomial distribution formula.
You will see that it looks alike.
HURRAH..!!! we just proved our formula.

The END#