This problem mainly occurs when there is large number of layers in the neural network. As from the previous blog we understood that weights in deep neural networks are updated using the equation as shown

let's mark this equation as equation no. 1
during the back propagation.

Before proceeding further it is very much important to know what is activation function and where it is used.

What is Activation Function?#

Activation functions are mathematical equations that determine the output of a neural network. This functions are added to each neuron in the neural network and determines whether it should be fired or not, based on neuron’s input.

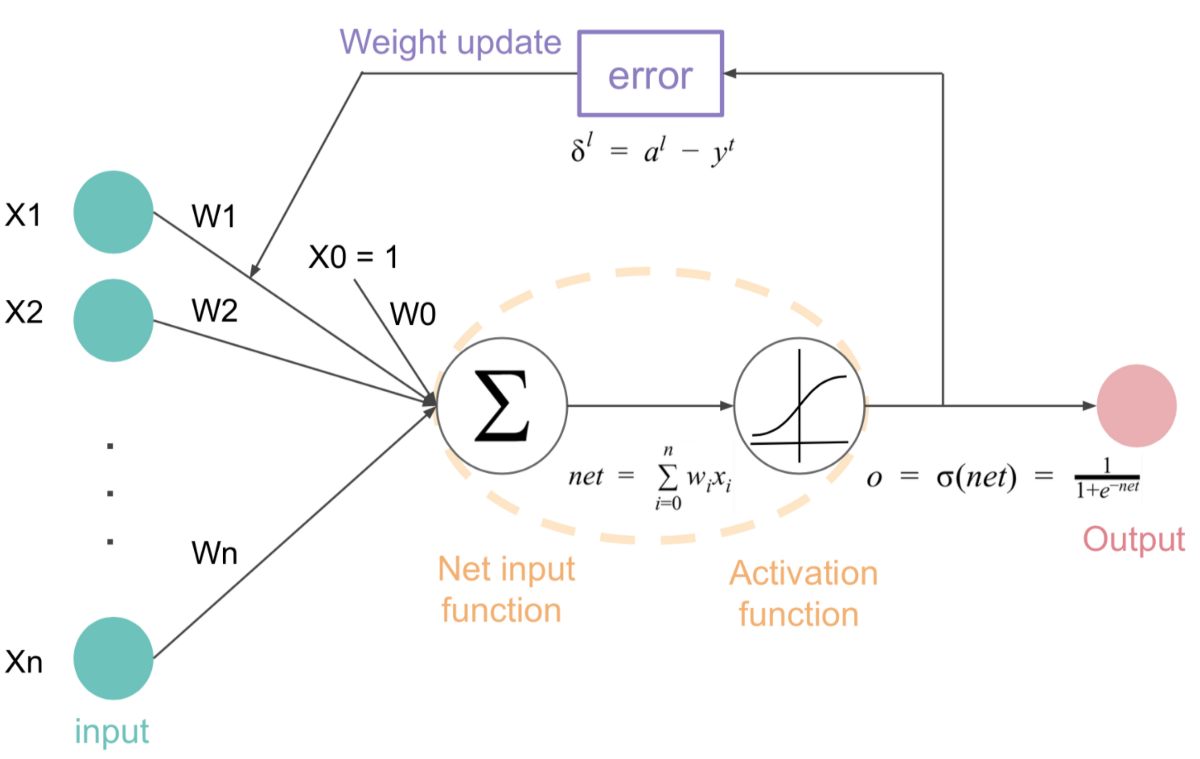Activation Function in Deep Learning Image Courtesy

Where is Activation Function used?#

You must have seen this equation in the earlier blog so we have to add activation function to this equation

And the updated equation looks something like this.

let's mark this equation as equation no. 2

There are various activation function like Sigmoid, Tanh, Relu, Leaky relu etc. which we will discuss in upcoming blogs.

Understanding vanishing gradient problem#

As from equation no. 1 we can see derivative of loss is taken so when we calculate the updated weight during back propagation value of this derivative function become extreme small and so weight is also updated by a very small value. And as the layer of the neural network increases this updation of weight is negligible (almost zero) and this problem is called as vanishing gradient problem.

But now you must be having a question why weight updation are decreasing?

To answer this question will refer the below plot here we can see that the derivative of the sigmoid activation function lies between 0 to 0.25.

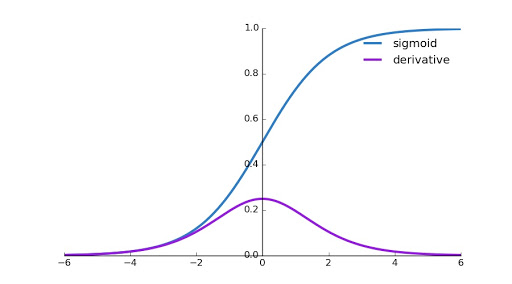Sigmoid Activation Function Image Courtesy

From equation no. 1 we can see that derivative of a loss function is taken. Loss function is nothing but difference y-predicted and y-actual and in this y-predicted there are activation function added which you have seen earlier in equation no. 2

While calculating updated weight the value of this part of the equation decreases which in turn leads to small amount of weight updation.

When there are large layers of neural network we use derivative's chain rule to calculate the updated weights so when the derivative of sigmoid function is multiplied the weight updation becomes very less. And it goes on decreasing as we proceed from last layer to initial layer.

And in the initial layer weight updation is negligible. We know that how important our initial layer are as they are the ones to which input is given and if weights are not updated properly in this layer then the our model will not be able to predict the output correctly.

The END#